The population P(t) of a culture of the bacterium Pseudomonas aeruginosa is given by
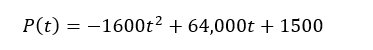
where t is the time in hours since the culture was started.
a) Determine the time at which the population is at a maximum.
Round to the nearest hour.
b) Determine the maximum population.
Round to the nearest thousand.
Quadratic Function Background
What is a quadratic function?
A quadratic function is an equation with a degree of two.
The general form of a quadratic is
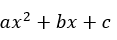
where a, b, c are all real numbers and a can't equal zero.
The parabola
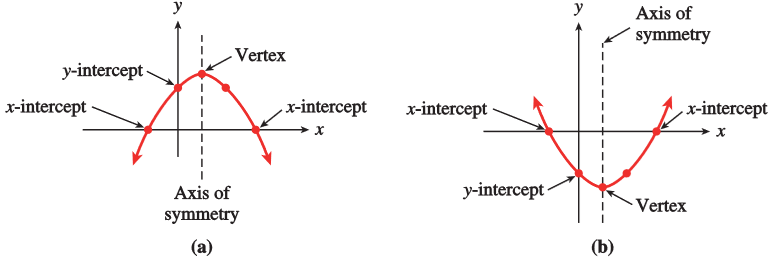
The graph of a quadratic function is a U-shaped curve which is called a parabola. The highest or lowest point on the parabola is called the vertex.
If the parabola opens up, the vertex represents the lowest point on the graph. If the parabola opens down, the vertex represents the highest point on the graph.
The standard form of a quadratic equation is
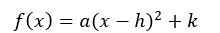
, where the vertex is (h,k).
The vertex (h,k) is located at
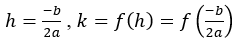
, where k is the output value of the function when the input is h.
h is considered the horizontal coordinate, also known as the x-coordinate
k is considered the vertical coordinate, also known as the y-coordinate.
Maximum or minimum of the parabola
The vertex of the quadratic formula can be a maximum or minimum depending on the orientation of the parabola. If the parabola is facing downward (figure a), the vertex is the highest point (at a maximum). k is the maximum functional value, it occurs when x = h. If the parabola is facing upward (figure b), then the vertex is on the lowest point ( at a minimum). k is the minimum functional value, it occurs when x = h.
In the general form of the quadratic function,
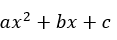
the parabola is facing downward when a is negative(figure b). When a is positive, the parabola is facing upward(figure a).
We want to find the vertex of a parabola because this point will inform us what the maximum or minimum output value, (k) and where it occurs (h).
Solving the Problem
a) Determine the time at which the population is at a maximum. Round to the nearest hour.
The equation
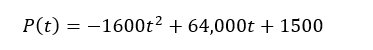
where
a=-1600
b=64,000
c=15,000
Since a is negative, the parabola for this equation faces downward, giving us a maximum.
Find the vertex which is the x-coordinate(h) of the equation to find the maximum time.
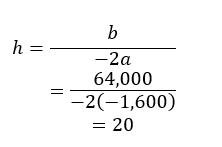
The time the population is at a maximum is at 20 seconds.
b) Determine the maximum population. Round to the nearest thousand.
Remember the output value (k) of the function when the input is h.
k is also known as the y-coordinate
To determine the maximum population find the y-coordinate (k).
We found the maximum time in part a. which is
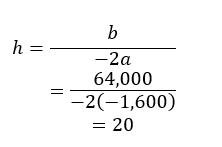
Plug 20 in for t into the equation
The maximum population is 655,00.